FÍSICA E ESPORTE

Marcelo Andrade de Filgueiras Gomes

 

Em 2005 se comemora não apenas o Ano Internascional da Física, mas também o Ano Internacional do Esporte e da Educação Física. A física, como esperado, controla o que uma pessoa pode ou não fazer em termos de esportes. Neste trabalho, discutiremos aspectos físicos fundamentais relacionados à prática esportiva. Menos esperado é o fato de que muito da física relevante ao esporte é objeto atual de pesquisa e também fonte de controvérsias importantes. Considerações físicas da maior relevância nessa área, tais como hipóteses de escala e de resistência dos materiais, nasceram com a própria ciência física no século XVII, como se constata no último e mais importante livro de Galileo Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze, publicado em Leiden, em 1638.

A POTÊNCIA Problemas não-triviais já aparecem ao nível da potência P dissipada por um organismo vivo em repouso (potência basal). Essa quantidade, ou taxa de perda de calor, dQ/dt, para um animal de tamanho característico L, escala com a sua área total A: P ~ A. Usando A~L² e massa = M~L³, temos P ~ M^2/3. 1

Desde 1930 os fisiologistas (1) fizeram medidas precisas do dispêndio energético em animais em função da massa corporal, encontrando:

P (Watts) = 3,6M(kg)^0,73 (Lei de Kleiber), 2

para quase seis décadas de variação de M. Assim, uma pessoa de 70kg consome, em média 80Watts de potência. Uma explicação da origem da equação 2 foi dada em 1973 por McMahon (2), assumindo as hipóteses: (i) a massa do animal é dada pela soma de massas distribuídas em partes cilíndricas de comprimento L e diâmetro d, i.e. M~L´d ², e (ii) L~d ^2/3, implicando em M~d ^8/3. Por outro lado, pela Lei de Hill da potência muscular, P escala com a força muscular F, i.e. com d ², e daí P~d ²~M ^3/4, resultado muito próximo ao encontrado experimentalmente por Kleiber. Esta última expressão é, no entanto, diferente de 1, pois o expoente da lei de potência é 12,5% maior.

Em 1997, West, Brown e Enquist (3) apresentaram uma segunda argumentação para justificar um expoente 3/4 na lei da potência dissipada, em detrimento do expoente 2/3, como exposto na equação 1. O modelo desses autores baseia-se na minimização da energia dissipada no transporte de nutrientes por uma rede ramificada interna de tipo fractal (o sistema vascular do animal). Dois anos após, Banavar, Maritan e Rinaldo (4), também chegaram a P~M ^3/4, mas usando hipóteses diferentes às das referências 2 e 3, a saber minimizando o volume total de nutrientes (sangue) e sem necessidade de assumir estruturas tipo-árvore para o sistema vascular. Surpreendentemente, em 2001, Dodds, Rothman e Weitz (5) reanalisaram todos os dados experimentais disponíveis de potência basal versus massa para mamíferos e pássaros, bem como revisaram todas as justificativas teóricas que fornecem o expoente 3/4 na equação 2, chegando à conclusão de que existe pouca evidência, de fato, para se rejeitar a equação 1. Segundo eles, a lei de escala da potência basal pode ser complexa mas, se tal lei existir num amplo intervalo de variação de massa, terá pouca chance de que o expoente seja 3/4.

A potência basal é controlada por três constantes físicas fundamentais: a constante de Boltzmann, k_B , a constante de Planck, h e a velocidade da luz no vácuo, c. Para justificar isso, basta lembrar que o corpo humano funciona como uma fonte de calor à temperatura fisiológica de aproximadamente T_f =309K. Supondo esse corpo mergulhado no meio ambiente à temperatura T, haverá um fluxo de calor, do corpo para o meio ambiente se T<T_f , e na direção contrária se T>T_f , sendo que a primeira situação em geral prevalece. A taxa com que o calor ou a energia flui do corpo para o ambiente, dE/dt, é dada pela Lei de Stefan-Boltzmann (6):

dE/dt = b x e x A ´ (T_f ⁴ – T ⁴), 3

onde a constante de Stefan-Boltzmann, b=2p⁵k_B⁴/15h³c² vale 5,7 ´ 10^-8Wm^-2K ^-4; e é a emissividade e A é a área que emite radiação. Para um adulto humano, A » (1,4±0,2)m², de tal sorte que a equação 3 nos dá, com e=1 e T=300 K, dE/dt » (80± 10)W, em concordância com a equação 2. Ao multiplicarmos este valor pelo número de segundos em um dia, achamos (1650±200)Cal (1Cal=1000cal) para a energia mínima necessária à sobrevivência de um adulto, i.e. para repor apenas as perdas por radiação. Esta quantidade se constitui na maior fração de nosso consumo energético diário; ou seja, temos um baixo rendimento termodinâmico.

Os adultos podem dispor de potências bem maiores do que 80W mas, em geral, quanto maior a potência numa atividade, menor será o tempo de que dispomos para empregá-la; assim, uma pessoa bem condicionada poderá dispor de 1,09HP (802W) durante 1 minuto, e de uma potência de 1,87HP (1375W) durante 10 segundos. Uma das taxas fisiológicas mais importantes é a potência específica máxima disponível a um ser humano; esta vale j= 41,56 W/kg=0,0565HP/kg; ou seja, 3,9HP para uma pessoa de 70kg (7). Tal nível de potência só pode ser mantido pelo tempo de cerca de um segundo, podendo levar à morte uma pessoa não-preparada. Essa potência-limite é usada na largada das corridas de 100m e 200 m rasos, e no momento do arranque nas provas de levantamento de peso, nas quais o levantador tem um tempo da ordem de 1 segundo para levantar uma massa tipicamente de 140kg a uma altura acima de sua cabeça com os braços esticados.

 

 

A CORRIDA Ao andar, cada pé toca o chão por cerca de 40% do tempo, enquanto numa corrida a 5m/s e 9m/s esta fração cai respectivamente para 30% e 20%. Numa corrida olímpica curta, o tamanho do passo é muito maior, alcançando tipicamente 2,4m no regime de velocidade próximo a 10m/s (8). Enquanto no andar a velocidade escala com a raiz quadrada da altura L da pessoa (6), na corrida a velocidade máxima independe de L. Para mostrar como isso é possível em geral; considere um mamífero de massa M que sai do repouso e atinge a velocidade máxima V após certo tempo. A velocidade média é áuñ = V/2 e a potência média na corrida áPñ=áuñáFñ; portanto, usando os argumentos do segundo parágrafo, V~ áPñ ¸áFñ ~d ²/d ²~ d ⁰~L ⁰. Para uma espécie fixa, teríamos V=K´L ⁰, com K dependente da espécie. Se a velocidade máxima fosse crescente com L, a evolução já teria se encarregado de eliminar a variabilidade de tamanho observada dentro das espécies, privilegiando apenas os animais de maior porte. Devemos nos lembrar, ainda, de que muitos dos melhores corredores olímpicos são de estatura relativamente baixa.

Dentre os quadrúpedes, os mamíferos chitá e gazela, os quais formam um par predador-presa, são os campeões na corrida, alcançando respectivamente velocidades máximas de 30,5m/s (110km/h) e 28m/s (101km/h). Outros pares de predador-presa, como raposa/coelho e lobo/raposa, possuem velocidades máximas próximas, corroborando o velho ditado "Um dia é da caça e o outro do caçador". O caso da avestruz, que alcança 23m/s (83km/h), serve como contra-exemplo para afastar a "explicação" de que o homem (V_máximo »12,5m/s ou 45km/h) corre bem menos do que muitos animais por ser bípede. Ao longo da evolução as avestruzes, bem como todos os grandes corredores, como chitás e gazelas, transferiram para os respectivos troncos muito da massa muscular necessária para a corrida, deixando suas pernas desproporcionalmente muito mais leves do que as pernas humanas. Animais com pernas pesadas, como o homem, pagam um alto custo energético simplesmente para colocá-las em movimento acelerado. Atentos a esses detalhes, os treinadores dos corredores olímpicos de 100m e 200m, as provas mais rápidas de corrida, vêm realizando nas últimas décadas um verdadeiro trabalho de reengenharia muscular, cujo resultado é o de fortalecer muito a massa muscular do tronco e os ligamentos perna-tronco desses atletas. Muitos especialistas acreditam que a barreira para o homem alcançar maiores velocidades nas provas olímpicas é mais psicológica do que fisiológica (9); segundo eles, os melhores corredores um dia poderão correr tanto quanto as avestruzes.

A velocidade média ·áuñ na corrida depende evidentemente da distância D a ser percorrida: corridas longas (curtas) têm ·áuñ menor (maior), pois os corredores conseguem manter uma velocidade máxima por tempo muito limitado. As provas olímpicas de corrida são para oito valores de D, a saber: 100m, 200m, 400m, 800m, 1.500m, 5.000m, 10.000m e 42195m (Maratona), cobrindo uma variabilidade de 2,625 décadas em D. Assumindo uma força resistiva proporcional à velocidade, o matemático J. Keller mostrou em 1973 (7), que a estratégia otimizada para vencer a corrida de 200m consiste em se alcançar a velocidade máxima, de cerca de 11m/s, em aproximadamente 3,5s, e daí em diante manter essa velocidade máxima (atualmente os corredores não conseguem manter a velocidade máxima nesse trecho). Para os 400m, a estratégia otimizada consiste em atingir a velocidade máxima, de cerca de 9,5m/s, em pouco menos de 2,5s, e de manter essa velocidade até 0,86s antes da linha de chegada. Nos últimos 0,86s dessa corrida, a reserva de energia do atleta deve ser essencialmente zero, e sua velocidade deve cair do máximo para cerca de 6,7m/s ao terminar a prova. Podemos observar que o estado do corredor ao final dessa prova é muito diferente daquele observado nas provas de 100m e 200m: na primeira, o corredor chega quase desabando, devido a falência energética; ao passo que nas duas últimas percebemos que os corredores poderiam correr ainda um pouco mais sem variar muito o ritmo. Durante as provas curtas, o atleta usa, além da respiração, a reserva de oxigênio previamente armazenada nos tecidos. Na conclusão de uma corrida de 400m, ao contrário, já não existe mais oxigênio nos tecidos. A previsão teórica de Keller para o tempo mínimo da corrida dos 200m é de 19,25s (7), enquanto o recorde atual é 19,32s, obtido por Michael Johnson (USA), em Atlanta, 1996. Keller também mostrou que existe uma distância crítica, D_c=291m, tal que para corridas com D < D_c o atleta deve atingir a velocidade máxima, e daí em diante manter essa velocidade até o final; enquanto nas corridas com D > D_c, o atleta deve acelerar ao máximo por um tempo entre 1s e 2s, chegando ao final desse tempo a um regime de velocidade constante o qual deve ser mantido até 1s ou 2s antes do final da prova, quando deverá desacelerar. Em 1997 Mureika (10) estendeu a teoria de Keller, introduzindo a perda de energia do atleta nas curvas, um aspecto importante nas corridas de 200m e 400m.

No estudo dos recordes olímpicos de corridas, foi encontrada recentemente uma lei de escala (ainda não-explicada), a qual relaciona o tempo recorde de duração da prova, t_rec, com D (no intervalo 100m < D < 42.195m) em todos os tipos de provas: t_rec =A´D^a, com a=1,11±0,01, tanto para recordes femininos (A=0,068), quanto para masculinos (A=0,057) (6, 11). Esta lei de escala mostra que todas as estratégias completamente diferentes para se ganhar as diferentes provas de corrida vinculam-se a um mesmo princípio hierarquicamente superior.

 

 

A ACELERAÇÃO Usando a terminologia do segundo parágrafo, devemos esperar que a aceleração a disponível a um animal de tamanho L escale como: a=(F/M) ~ (d ²/Ld ²) = L ^-1. Ou seja, quanto maior o animal, menor a aceleração. Mamíferos como gatos e leões tem pernas muito musculosas, as quais privilegiam a aceleração no momento do bote, em detrimento da velocidade; gazelas têm pernas muito finas, as quais privilegiam a manutenção da velocidade máxima durante muito mais tempo, em detrimento simplesmente da aceleração. Por essa razão, leões (gatos) têm, na caça, apenas alguns segundos para alcançar gazelas (ratos). O chitá, o rei das corridas, também não consegue manter a sua velocidade por muito tempo; esse animal vai do repouso a 108km/h em 3s, o que dá uma aceleração de 10m/s², maior do que a da gravidade e a dos carros de corrida. Comparativamente à pulga, que alcança 2m/s em apenas 0,0015s, com aceleração de 136g (12), o chitá tem uma aceleração insignificante! Nas corridas olímpicas de 100m e 200m, a arrancada inicial, fase de grande aceleração, ocupa uma grande fração do tempo total da prova: cerca de 20% do tempo total para a de 200m e 40% para a de 100m. Assim, os músculos das pernas dos atletas que se dedicam a esses dois tipos de corridas têm uma preparação bem diferente das demais modalidades. Corredores que aspiram medalha de ouro nas provas olímpicas de 100m e 200m devem ser capazes de acelerar a 8m/s², no primeiro segundo após a largada; ou seja, devem dispor de uma potência específica perto do limite j=0,0565HP/kg definido no quinto parágrafo.

O PULO Pular tem grande importância no esporte e também na sobrevivência de outros animais. No pulo vertical, o animal retrai as pernas de forma a abaixar o seu centro de massa (CM) de uma altura y. Na hora do pulo, uma força muscular F age ao longo dessa mesma distância e produz um trabalho W=F ´y, o qual faz com que o CM alcance, com velocidade final zero (ponto de retorno), uma altura H>y acima da posição relaxada normal, ou seja, quando o CM está a uma altura y +H acima da posição mais retraída inicial. Conservação da energia para um animal de peso Mg leva ao trabalho feito W=F ´y=M´g´(y+H); portanto, a altura do pulo, y+H=(F´y)/Mg~(d²´L)/(Ld²) =d ⁰L⁰, i.e. independe da altura do atleta, como já observado para a velocidade máxima nas corridas. Por isso, jogadores baixos podem ser excelentes na hora de pular para cabecear, encestar ou cortar uma bola. A maior parte dos animais realiza pulos com H>>y; gatos, por exemplo, conseguem facilmente H/y=20. O homem é exceção: na melhor das hipóteses consegue H 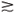y. Para o caso típico de um atleta com 70kgf, retraindo a sua altura de y=0,30m e tomando H=0,60m, temos: F=Mg(y+H)/y=3Mg. Considerando que a distensão dos músculos, e conseqüentemente F dure t=0,25s (8), temos para a potência dissipada:P=Mg(y+H)/t=2470W ou 3,4HP, praticamente o limite máximo de potência para essa pessoa. Como corolário, nenhum atleta consegue dar dois grandes pulos em seguida.

A RESISTÊNCIA Como em todos os materiais, o módulo de compressibilidade do osso, Y, é controlado por duas constantes físicas fundamentais: a constante de Planck e a massa do elétron (13). Tal fato e outros poucos detalhes implicam que Y para a matéria condensada esteja sempre entre 10¹⁰Pa e 10¹¹Pa (1Pa=1Pascal=1Newton/m²). Já o módulo de ruptura, R, em geral, é cem a mil vezes menor do que Y. Comparativamente a outros animais, o ser humano possui os ossos mais fortes; mesmo assim, providência especial tem que ser tomada para amortecer a queda de atletas em muitas competições, como no salto com varas, onde as alturas excedem 6m acima do chão. O osso humano mais vulnerável na queda vertical é a tíbia, cuja menor seção transversal no adulto vale s»3cm². Sendo o módulo de ruptura da tíbia R=1,7´10⁸N/m², ela tenderá a fraturar-se quando submetida a forças maiores do que sR»50.000N. Duas tíbias suportam no limite F_c=2sR=10⁵N, cerca de 130 vezes o peso de uma pessoa de 75kgf. Assim, as duas tíbias suportam uma aceleração de até 130g no impacto vertical com o piso. Se um atleta em queda de uma altura H amortecer o impacto, diluindo a desaceleração ao longo de uma distância y (por exemplo, flexionando as pernas), devemos ter H<F_c´y/Peso=130y, para não haver fratura das tíbias. Para y=1cm, como no impacto com o chão com as pernas essencialmente rígidas, uma altura H=130cm já implicará no risco de quebra das tíbias. Noutro extremo, se a desaceleração ocorrer ao longo de y=0,6m, o limite para a queda de risco subirá para H=78m, o qual parece superestimado – mas não é! Na realidade, o que ocorre é que nos saltos as desacelerações são exercidas quase que inteiramente sobre os tendões e ligamentos, os quais tem resistência à ruptura cerca de 1/20 em relação ao osso. Isso reduz a altura máxima, H_max, para colidir com o solo, a cerca de 78m/20=3,9m. O aspecto mais perigoso nas quedas de grandes alturas se refere ao fato de o corpo humano tender a girar e a cabeça, devido ao peso, tender a colidir com o chão.

A NATAÇÃO Em meio denso como a água, o empuxo anula o peso; conseqüentemente, a velocidade máxima V, no caso da natação, não pode depender explicitamente da massa. Diferentemente das corridas, a resistência ao meio, 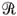, é importante aqui e esperamos que V dependa da quantidade de trabalho por ciclo, W, de 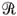, além da aceleração da gravidade g, pois quanto menor g, maior a dificuldade do nadador avançar; em particular, no limite g ® 0, não pode haver natação! Se V=V(g, W, 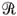) ~ g^g´W ^d´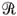^u, encontramos através de análise dimensional que g = d = -u = 1/2, ou seja: V ~g^1/2´(W/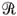)^1/2. Na mecânica dos fluidos, esta é a Lei de Froude da correspondência de velocidades (14). Tomando W=(Força muscular ´ deslocamento)~L²´L e 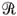~L², obtemos V~L^1/2; ou seja, a natação privilegia atletas de maior estatura, como constatamos nas raias das piscinas.

As provas olímpicas mais rápidas de natação são as de nado livre, em cinco distâncias: 50m, 100m, 200m, 400m e 1.500m. A velocidade média recorde nessas provas é de 2,282m/s, nos 50m, i.e. pouco mais do dobro da velocidade no andar de um adulto. Os tempos dos recordes olímpicos nas diversas provas de nado livre, t_rec, satisfazem uma lei de escala envolvendo a extensão do percurso, D: t_rec ~ D^1,09, para 50 < D < 1500 (6). Reexaminando este tipo de lei de escala já encontrada no caso das corridas, Savaglio e Carbone mostraram (15) que a velocidade média recorde, v_recºD/t_rec, quando expressa em função de t_rec apresenta claramente duas leis de escala controladas por dois expoentes críticos diferentes, os quais são interpretados como pertencendo aos regimes metabólicos de consumo de energia anaeróbico (provas curtas, com duração inferior a 150s-170s) e aeróbico (provas longas) pelos atletas.

CONCLUSÃO Em 1925, o melhor tempo nos 100m rasos foi 10,37s; hoje o recorde continua sendo o de 9,84s, obtido por Donovan Bailey (Canadá), em Atlanta: uma redução de 0,53s (5,1%) em 80 anos. No mesmo período, para os 400m, passamos de 46,94s para os 43,49s de Michael Johnson (EUA), também em Atlanta. Apesar de lentamente, os recordes olímpicos mudam; eles mudam como a tecnologia ligada ao esporte muda e como a tecnologia em geral muda. Já as leis de escala discutidas aqui não mudarão, pois elas são exemplos de limitações básicas impostas pelas leis físicas.

 

Marcelo Andrade de Filgueiras Gomes é professor do Departamento de Física da Universidade Federal de Pernambuco(UFPE), em Recife.

 

 

REFERÊNCIAS BIBLIOGRÁFICAS

1. Kleiber, M. Hilgardia, 6, 315. 1932.

2. McMahon, T. Science, 179, 1201. 1973.

3. West, G. B., Brown,J. H. and Enquist, B. J. Science, 276, 122. 1997.

4. Banavar, J. R., Maritan, A. and Rinaldo, A. Nature, 399, 130. 1999.

5. Dodds, P. S., Rothman,D. H. and Weitz, J. S., J. theor Biol. 209, 9. 2001.

6. Gomes, M. A. F. e Parteli, E. J. R. Rev. Bras. Ens. Fís. 23 (1), 10. 2001.

7. Keller, J. B. Phys.Today 26 (9), 42. 1973.

8. Cross,R. Am. J. Phys. 67, 304. 1999.

9. Ryder, H. W., Car, H. J. and Herget, P. Sc. Am. 234 (6), 109. 1976.

10. Mureika, J. R. Can. J. Phys. 75, 837. 1997.

11. Katz,J. S. and Katz,L. J. Sports Sci. 17, 467. 1999.

12. Rothschild, M., Schlein, Y., Parker, K., Neville, C. and Sternberg, S. Sc. Am. 229 (5), 92. 1976.

13. Weisskopf, V. F. Science 187, 605. 1975.

14. Thompson, D. W. On growth and Form. New York, Dover. 1992.

15. Savaglio, S. and Carbone,V. Nature 404, 244. 2000.