MUNDO

 

Interferência da luz, arte e computação

 

 

Stephen Walborn

Físico, professor do Instituto de Física da Universidade Federal do Rio de Janeiro (UFRJ) e coordenador do Laboratório de Ótica e Informação Quântica da UFRJ. Email: swalborn@if.ufrj.br

 

 

A luz é uma onda eletromagnética. E, como todas as ondas, ela exibe fenômenos naturais que são distintos daqueles observados com objetos corpusculares, tais como uma partícula ou uma bola de gude. Essa divisão entre corpúsculos e ondas é um tema central na física. Conhecemos muito bem o comportamento de um corpúsculo no nosso dia a dia. Imagine uma bola de futebol quicando no chão. Observando a altura de um quique, podemos já prever, mentalmente, a altura do próximo quique, baseado simplesmente em nosso conhecimento prévio. Já os fenômenos ondulatórios são menos conhecidos, embora amplamente presentes no nosso cotidiano. Imagine agora uma onda do mar, que vem lá do fundo e quebra na areia da praia. Sentado na praia, notamos que durante um intervalo de tempo vem ondas grandes, depois vem ondas menores e, às vezes, passa um período no qual não vem nenhuma onda. Depois, voltam a vir as ondas grandes, e tudo se repete. Este é um exemplo do efeito de interferência. As ondas no mar são criadas por diversos tipos de perturbações na água. A causa principal é o vento, que empurra a superfície da água, criando ondas paralelas a ele. Acontece que, em certa região do mar, pode-se encontrar ondas vindo de várias fontes e essas ondas interferem entre si. Se duas ondas se encontram, de tal forma que a crista de uma coincide com a crista da outra, essas ondas se somam formando uma onda maior. Chamamos essa situação de interferência construtiva. No entanto, se as ondas se encontram, de tal forma que a crista de uma coincide com o vale da outra, essas ondas se cancelam e temos interferência destrutiva. Esses fenômenos que observamos na praia são devidos às interferências de ondas.

A interferência de ondas também é observada com a luz. Isso foi demonstrado pela primeira vez em um lindíssimo experimento realizado em 1803 pelo inglês Thomas Young. Ele iluminou um papelão, o qual continha um corte de duas fendas estreitas (do tamanho de um cabelo humano) e muito próximas, de tal forma que a luz só passava pelas fendas (figura 1a). Ele observou que, em um ponto, suficientemente distante das fendas, as ondas originadas das duas fendas interferiram entre si, produzindo um padrão alternado de listras brilhantes e escuras. Ou seja, as ondas que se encontravam construtivamente produziam uma listra brilhante, e as ondas que se encontravam destrutivamente produziam uma listra escura. Uma foto de um experimento de Young é mostrada na figura 1b.

 

 

O experimento de Young, conhecido como "o interferômetro de fenda dupla", também pode ser realizado com mais de duas fendas. Nesse caso, observamos o padrão de interferência ilustrado na figura 1c, que é o resultado da interferência entre todos os possíveis pares de ondas que se encontram na região de observação. Por exemplo, se houver três fendas produzindo ondas, A, B e C, o padrão que observamos vai depender da interferência de A com B, de B com C, e de A com C. Assim, numa distância após a fenda tripla, haverá regiões nas quais essas três interferências são todas construtivas, resultando listras muito brilhantes. E, em outros lugares, haverá interferências distintas; por exemplo, duas construtivas e uma destrutiva, havendo uma intensidade de luz reduzida, ou até nula, formando o padrão de interferência da figura 1c. A mesma lógica se aplica quando há um aumento no número de fendas. Em algumas regiões, vemos listras bem brilhantes, onde todos os pares de ondas interferem construtivamente. Em alguns pontos, vemos uma intensidade nula e em outros uma intensidade bem baixa ou nula.

Agora imagine o caso extremo desse interferômetro de Young, no qual temos um número infinito de fendas iluminadas pela luz. Novamente, teremos algumas regiões de observação nas quais todas as interferências entre os pares de ondas interferem construtivamente entre si, formando "máximos" de intensidade. Porém, na maior parte do tempo, teremos algumas interferências construtivas e outras destrutivas entre os pares de ondas. Como são muitas ondas, a intensidade que observamos nestes pontos é muito menor do que a intensidade da luz nos máximos de interferência. O que vemos na região de observação são somente os pontos de interferência construtiva, como ilustrado na figura 1d.

Uma abertura com um número muito grande de fendas é conhecida como uma rede de difração, ou grade de difração. Observamos a difração quando olhamos o lado inferior de um disco CD ou DVD, por exemplo. A luz multi-colorida que vemos é a luz branca difratada pelos trilhos do disco. Como o ângulo de difração é diferente para cada cor, a difração na grade separa a luz branca nesse arco-íris.

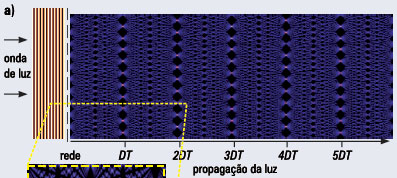
Esses efeitos de interferência e difração são observados em pontos de observação que são muito distantes da abertura, em comparação com a distância entre as fendas e o comprimento de onda da luz. No entanto, um dos efeitos ondulatórios mais bonitos aparece quando observamos a difração da luz muito perto de uma grade de difração. Devido à periodicidade da grade, em distâncias curtas, a interferência construtiva resulta numa imagem nítida da própria grade de difração iluminada. Este é um efeito de autoimagem por interferência conhecido como o efeito Talbot, em homenagem ao Henry F. Talbot, que observou esse fenômeno pela primeira vez em 1836 (1). A distância entre a grade e a primeira autoimagem é conhecida como a distância de Talbot (DT) e todas as autoimagens aparecem em distâncias que são múltiplos inteiros de DT. Se a distância de observação for um múltiplo par de DT (2DT, 4DT,...), a imagem observada é idêntica à da grade. Se a distância de observação for um múltiplo ímpar de DT (DT, 3DT,...), uma autoimagem é observada, porém esta é deslocada por metade da distância entre as fendas. O resultado dessa duplicação da grade é o padrão de intensidade bonita mostrada na figura 2a. Podemos ver na figura uma estrutura complexa que lembra um tapete persiano e, por isto, esse padrão de interferência é conhecido como o "tapete de Talbot" ou "tapete de luz". De fato, a estrutura desse tapete de luz é ainda mais complexa do que simples autoimagens. Por exemplo, se olharmos a meia distância de Talbot da grade, DT/2, observamos um padrão de intensidade que parece uma réplica da própria grade, só com a distância entre os pontos brilhantes reduzida pela metade. Essa imagem, de fato, é uma superposição da imagem original com a imagem deslocada. Se olharmos a uma distância DT/3, vemos uma réplica com período reduzido por um fator três, que corresponde a uma superposição de três cópias da imagem, deslocadas entre si. Para qualquer distância de observação, que pode ser escrita como p/q DT, onde p e q são números inteiros, vemos um padrão de difração composta de q cópias da imagem da grade deslocadas.

 

 

Essas imagens e réplicas que formam o bonito tapete de luz, mostrado na figura 2a, são evidências de uma estrutura matemática complexa e muito bonita. Recentemente, em colaboração com os pesquisadores Osvaldo Farías, Fernando de Melo e Pérola Milman, percebemos que o efeito Talbot poderia ser utilizado para realizar portas lógicas para processar informação (2). Alguns exemplos de como processar informação com a ótica serão discutidos abaixo. Um aspecto interessante do nosso trabalho é que a computação pode ser observada através de tapetes de luz, como aqueles ilustrados nas figuras 2a, 2b e 2c. Essas imagens são exemplos muito simples da evolução de diferentes condições iniciais do campo de luz que incide na rede de difração. Ao desenvolver o trabalho, vimos que, no mínimo, o nosso "computador de Talbot" é capaz de produzir figuras muito lindas.

Efeitos de interferência de muitas fendas são intimamente relacionados com a matemática. Em 1995, os pesquisadores norte-americanos John Clauser e Johnathan Dowling mostraram que, em princípio, seria possível utilizar a interferência da luz para achar os fatores de um número (3). O objetivo na tarefa de fatoração é decompor um número N nos seus fatores primos. Um número primo P é um número cujos únicos fatores são 1 e o próprio P. Assim, podemos fatorar o número 429 no produto de números primos: 429=13x11x3. Na matemática, acredita-se que a fatoração é um problema difícil. Em outras palavras, o tempo necessário para achar os fatores de um número N cresce, rapidamente, com o tamanho do número N. Por exemplo, é possível achar os fatores de 429 com facilidade em poucos minutos com um pedaço de papel e uma caneta, porém, achar os fatores de 10.079.445.923 é muito mais difícil. Por outro lado, é fácil verificar se um conjunto de números são os fatores de N, pois a multiplicação é fácil. Levamos somente um minuto para verificar que 99839x100957 = 10.079.445.923. Hoje em dia, aproveitamos diariamente da dificuldade da fatoração, pois esse problema é o coração de algoritmos de criptografia de chave pública, que são muito utilizados na informática, por exemplo, para enviar o número do cartão de crédito de forma segura em compras feitas pela internet.

O tempo necessário para fatorar um número com um computador cresce exponencialmente com o tamanho do número. Como fatorar um número N usando a interferência? Imagine uma abertura de N fendas, onde N é um número grande cujos fatores queremos achar. Clauser e Dowling mostraram que, quando essa abertura é iluminada com um feixe de luz de intensidade constante, veremos uma réplica perfeita das fendas somente quando observamos o padrão de interferência a uma distância dada por mDT, onde m é um fator de N. Este é um efeito parecido com o efeito de Talbot, que agora se aplica a um número finito de fendas, N.

Então, por que não deciframos as comunicações seguras usando a interferência? Aqui, o nosso "cálculo" será realizado na velocidade da luz; neste sentido, não seria possível fatorar números muito rapidamente? Nesse caso, há um outro recurso que cresce exponencialmente com o tamanho do número. Os números usados tipicamente na criptografia, hoje em dia, têm centenas de dígitos. Por exemplo, vamos pegar um número muito humilde no contexto da criptografia, como N=10.079.445.923. Se a separação entre as fendas fosse de 1 micrômetro (aproximadamente um centésimo da largura de um cabelo humano) e se ignorarmos a largura de cada fenda, a abertura de N fendas teria 10.079.445.923 micrômetros de largura, que é por volta de 10 Km. Se N tivesse 150 dígitos, a abertura seria dez vezes maior do que o diâmetro da nossa galáxia! É exatamente por esta razão que dizemos que a fatoração é um problema difícil, já que o recurso necessário para resolver o problema (espaço, tempo, memória do computador etc) cresce exponencialmente com N. No caso da luz, o problema é o tamanho do feixe de luz e da abertura.

No final do século XIX, os cientistas perceberam que a luz é composta por pacotes indivisíveis de energia, chamados de "fótons". Esta ideia revolucionária faz parte da base fundamental da física quântica, a nova teoria desenvolvida no início do século XX para descrever a natureza no nível microscópico. Albert Einstein ganhou o prêmio Nobel da física em 1921 não por sua teoria de relatividade, mas sim por explicar o efeito fotoelétrico (emissão de elétrons de um metal excitado pela luz), postulando que a luz é composta de fato por fótons, ou "quanta" de energia. Um feixe de luz, como um laser ponteiro de cor vermelho, por exemplo, contém aproximadamente 10¹⁸ fótons.

O que acontece quando um fóton incide numa fenda dupla? Este experimento foi realizado em 1909 pelo cientista britânico Geoffrey Taylor (4). No campo distante das fendas, os fótons foram registrados em cima de uma tela fotosensível. Quando um fóton é detectado, ele aparece como um ponto na tela. Assim, com a detecção de um único fóton, não é possível observar nenhum padrão de interferência. No entanto, repetindo o experimento para registrar um número suficiente de fótons, vemos que os pontos na tela reproduzem o mesmo padrão de interferência que foi observado com a luz de um laser, como ilustrado na figura 1d. Esse experimento ilustra a natureza "dual" da radiação. Ao passar pela fenda dupla, o fóton se comporta como uma onda, produzindo um padrão de interferência. Porém, quando o fóton é detectado na tela, ele aparece de forma localizada, como uma partícula. Esta "dualidade" onda-partícula é um tema central na física quântica.

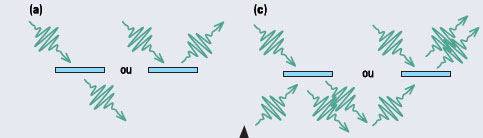
Todos os efeitos óticos que observamos com a luz de um laser ou de uma lâmpada comum, são bem explicados através da teoria da ótica clássica desenvolvida antes do século XX. Porém, novos efeitos aparecem quando tratamos de fontes de luz que emitem poucos fótons (figura 3). Por exemplo, imagine um semiespelho, um dispositivo que transmite metade da luz incidente e reflete a outra metade. O que acontece quando um fóton encontra um semiespelho? O fóton não se divide; então, ele deve passar ou ser refletido pelo semiespelho, como mostrado na figura 3a. Se colocarmos um detector em cada lado do semiespelho, somente um desses detectores registrará o fóton. Se repetirmos esse experimento muitas vezes, observaremos que o fóton é transmitido em 50% das vezes e refletido nos outros 50%. As leis da física quântica determinam que esse comportamento é totalmente aleatório. Ou seja, é impossível predeterminar por onde o fóton vai passar. Essa aleatoriedade é uma característica intrínseca da teoria quântica. Encontramos no dia a dia processos que parecem ser aleatórios, tais como a jogada de uma moeda. No entanto, nesses casos, é somente difícil prever o resultado, porém, não é impossível. Por exemplo, se soubéssemos todas as condições da jogada da moeda (força da jogada, massa da moeda etc) poderíamos, em princípio, prever se o resultado será "cara" ou "coroa" usando as leis da física clássica. Isso não é verdade para o caso do fóton. As leis da física proíbem a predeterminação do resultado. Dessa forma, o fóton incidente no semiespelho é uma moeda totalmente justa: é impossível prever se ele vai transmitir ("cara") ou vai refletir ("coroa"). Hoje em dia, há empresas que vendem "geradores de números aleatórios" baseados nesse princípio.

 

 

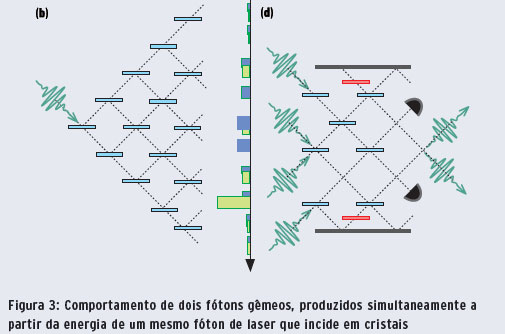
A diferença entre um fóton e uma moeda pode ser vista ainda melhor considerando uma "caminhada aleatória". Imagine que um amigo joga uma moeda. Se o resultado for cara, ele toma um passo para a esquerda. Se for coroa, ele vai um passo para a direita. Repetindo esse processo um número vezes, o seu amigo continua aleatoriamente para a esquerda ou para a direita cada vez que joga a moeda. No final, em média, como metade dos resultados da jogada deram cara e metade deram coroa, o seu amigo vai acabar a caminhada muito perto do lugar inicial. Um fóton, por outro lado, é capaz de realizar a "caminhada aleatória quântica", proposta pela primeira vez pelo físico isrealense Yakir Aharonov em colaboração com os físicos brasileiros Luiz Davidovich e Nicim Zagury (5). No esquema ilustrado na figura 1b, há um fóton incidente num semiespelho. No caminho de cada saída é colocado mais um semiespelho. Em cada caminho de saída destes, é colocado mais um semiespelho, e assim por diante. O fóton vai passar a refletir aleatoriamente em cada semiespelho, igual ao amigo com sua moeda. No entanto, observamos interferência entre as diferentes possíveis trajetórias do fóton pela sequência de semiespelhos. Vemos na figura 1b que o fóton poderia chegar em uma das saídas no centro por diversas trajetórias. Estas interferem entre si. Diferente do seu amigo, é mais provável o fóton terminar a caminhada aleatória longe do lugar que começou, como mostrado no histograma na figura 1c. A caminhada aleatória tem uma ampla gama de aplicações em modelagem de processos estatísticos, tais como o mercado financeiro, a difusão de partículas e foi até usada para desenhar a escultura "Quantum cloud", construída em Londres pelo artista plástico Antony Gormley em 1999.

A natureza apresenta grandes diferenças quando tratamos de um único fóton. Com dois fótons, a história se torna mais interessante ainda. Em alguns laboratórios do Brasil e do mundo, há cristais que, quando neles incide um laser, produzem um par de fótons "gêmeos". Esses fótons são chamados de gêmeos, pois são produzidos simultaneamente a partir da energia do mesmo fóton do laser, de tal forma que a soma das energias dos gêmeos é igual a energia do fóton parente. Devido aos outros vínculos no processo, os fótons saem do cristal com trajetórias distintas. Em 1987, os pesquisadores, Chung K. Hong, Zhe-Yu Ou e Leonard Mandel usaram espelhos para direcionar dois fótons com a mesma energia, de tal forma que eles chegaram simultaneamente em lados opostos de um semiespelho (6). O fóton incidente em cada lado pode ser transmitido para o outro lado ou refletido de volta. Desta forma, há quatro possibilidades: os dois fótons são transmitidos, ou os dois fótons são refletidos, ou um fóton é transmitido e o outro refletido, ou vice-versa. O que Hong, Ou e Mandel observaram foi que os fótons sempre "se agrupam", e saem pelo mesmo lado do semiespelho, como ilustrado na figura 3c. Note que os primeiros dois eventos correspondem aos casos nos quais há um fóton em cada saída do semiespelho. Vamos supor que no evento no qual os dois fótons são transmitidos pelo semiespelho, a amplitude é A. Assim, no evento no qual os dois fótons são refletidos, a amplitude é -A. O que observamos é sempre a soma das amplitudes de todos os eventos. Como A+(-A)=0, esses dois eventos interferem destrutivamente, e se anulam. Dessa forma, sempre observamos os dois fótons "agrupados" na mesma saída do semiespelho. Este é um efeito de interferência que depende, essencialmente, do caráter quântico da luz.

Embora o agrupamento determine que os fótons saem juntos pelo mesmo lado do semiespelho, é impossível predeterminar por qual lado eles vão sair, como no caso de um único fóton. Podemos pensar que é um experimento de lançamento de duas moedas que sempre retornam o mesmo resultado "cara" ou "coroa", aleatoriamente. Esse experimento é análogo a um experimento de fenda dupla, onde os dois fótons passam juntos por uma das fendas ou juntos pela outra. Em 1999, os pesquisadores brasileiros Eduardo Fonseca, Carlos Monken e Sebastião Pádua realizaram o experimento de fenda dupla com pacotes de dois fótons, chamados de "bi-fótons" (7). Eles observaram um padrão de interferência cujas oscilações variavam duas vezes mais rápido do que o padrão de interferência de cada fóton sozinho. O período de oscilação (distância entre listras brilhantes) é proporcional ao comprimento de onda da luz. Assim, podemos concluir que o comprimento de onda do bi-fóton é dado pela metade do comprimento de onda de cada fóton. Da mesma forma, um pacote de N fótons teria um comprimento de onda N vezes menor do que o comprimento de onda dos fótons componentes. Essa propriedade interessante tem aplicações em metrologia e litografia ótica, onde a precisão é proporcional ao período de oscilação da interferência. Ou seja, quanto menor o comprimento de onda, melhor a precisão. Esse fato se torna relevante em mídia digital, por exemplo. Um disco blue-ray contém muito mais informação do que um simples CD. Um blue-ray é lido com um laser com comprimento de onda 405 nanômetros, e um CD com laser de 780 nanômetros. Dessa forma, os poços e ilhas que codificam a informação em um blue-ray podem ficar duas vezes mais próximos do que em um CD, aumentando consideravelmente a quantidade de informação contida no disco.

A dualidade onda-partícula e a interferência de dois fótons são exemplos de propriedades quânticas da natureza. Em geral, efeitos quânticos aparecem somente quando tratamos de sistemas muito pequenos, compostos por poucos fótons ou poucos átomos, por exemplo. Em 1982, o físico norte-americano Richard Feynman sugeriu que sistemas quânticos poderiam ser úteis para processar informação (8). Uma das ideias iniciais do Feynman foi na área de simulação computacional de sistemas físicos, como uma cadeia de átomos, por exemplo. Ele notou que, para acompanhar a evolução de M sistemas quânticos, em geral, precisamos tomar conta da ordem de 2^M números complexos. Este é um crescimento exponencial que limita bastante as simulações numéricas que podem ser feitas por computadores clássicos. Assim, ele sugeriu que um computador que seguisse as leis da física quântica seria mais adequado para tal simulação. Com um simulador quântico composto de somente M sistemas controláveis no laboratório, poderíamos simular M outros sistemas quânticos sobre os quais não temos domínio. Alguns anos depois, foi demonstrado, de fato, que este "computador quântico" seria capaz de realizar algumas tarefas difíceis com um desempenho muito melhor do que qualquer computador que opera a partir das leis da física clássica. Um exemplo dessas tarefas é a fatoração de números, que poderia ser realizada eficientemente por um computador quântico. Isso deu partida para uma grande corrida científica-tecnológica em busca do computador quântico.

De onde vem o poder do computador quântico? Na computação, a informação é codificada em bits. Um bit de informação pode ser representado por um símbolo, que pode tomar dois valores, 0 ou 1, como um ponteiro que aponta para cima ou para baixo. Com M bits podemos representar 2^M números, de 0 a 2^M -1, por exemplo. Um sistema quântico de dois níveis, tal como um fóton que pode ser refletido ou ser transmitido por um semiespelho, também codifica um bit de informação. Aqui poderíamos fazer a associação "transmitir = 0" e "refletir=1". Além disto, um fóton pode ficar em um estado de superposição entre 0 e 1. Ou seja, depois do semiespelho, ele está, de fato, em uma superposição entre "transmitido" e refletido". Desta forma, o fóton representa um "bit quântico", um ponteiro que pode apontar para qualquer direção no espaço. Assim, M sistemas quânticos também podem representar 2^M números, que são possíveis estados do sistema. Mas, além disto, esses M sistemas podem existir em um estado de superposição desses 2^M números. Essa superposição de estados dá acesso a um "paralelismo quântico" que permite a realização eficiente de algumas tarefas de computação que são difíceis para computadores clássicos.

Os computadores são compostos de portas lógicas básicas, cujo papel é de transformar esses símbolos, de acordo com as instruções do usuário (o "programa"). Um resultado importante da teoria de computação clássica foi perceber quais portas lógicas são necessárias para o computador poder realizar qualquer operação lógica nos seus bits. Essas portas são conhecidas como "portas universais". Em 1989, o pesquisador australiano Gerard Milburn propôs um método de implementar a porta universal "Fredkin" entre fótons (9). Nesse esquema, um meio material com propriedades não-lineares é usado de tal forma que a presença ou não de um fóton controla a saída de um interferômetro. Essa foi a primeira proposta de implementação de uma operação lógica básica de um computador quântico com a luz. A grande desvantagem desse esquema é a necessidade de usar um meio não-linear, que é muito ineficiente, tornando o esquema inviável com a tecnologia de hoje.

Em 2001, Milburn, em colaboração com Emanuel Knill e Raymond Laflamme (KLM), propôs uma arquitetura para um computador quântico que funciona através da interferência de múltiplos fótons (10). Nesse esquema revolucionário, fótons são enviados por um grande conjunto de interferômetros que consistem simplesmente em elementos "lineares", tais como semiespelhos e placas de fase. Estas últimas são dispositivos óticos que permitem controlar a diferença de fase dentro dos interferômetros e determinam se a interferência será construtiva ou destrutiva. Os interferômetros funcionam como um grande "circuito ótico" para os fótons, em analogia com os circuitos eletrônicos. Por exemplo, imagine que há F fótons entrando num interferômetro com C caminhos e que C é maior do que F. A figura 3c ilustra uma porta lógica simples usando esse esquema. Dependendo do desenho do circuito, esses fótons poderiam seguir dentro do circuito ótico por diversos caminhos. Os fótons que se encontram juntos no mesmo semiespelho interfirão entre si. No final do circuito, os fótons poderão sair por diferentes combinações de portas de forma aleatória. O que KLM perceberam foi que seria possível desenhar o interferômetro de tal forma que os eventos nos quais temos somente um fóton em F saídas correspondam à realização de um conjunto de portas lógicas. Dessa forma, usando detectores em algumas saídas, é possível identificar um evento que corresponde ao programa que queremos "compilar". O que descrevemos aqui é um computador probabilístico, pois ele retorna o resultado desejado somente com uma certa probabilidade de sucesso. No caso de fótons, essa probabilidade pode ser muito pequena. Por exemplo, imagine que temos dois bits X e Y e queremos inverter o valor do bit Y somente quando o X=1. Usando quatro fótons e um interferômetro de oito caminhos, podemos realizar essa operação simples com uma probabilidade de sucesso de somente 6,25%. Até agora, o nosso computador quântico fotônico não parece nada fantástico. No entanto, no mesmo trabalho de 2001, KLM demonstraram uma forma de aumentar essa probabilidade usando mais fótons e mais interferômetros. A ideia básica é que as partes probabilísticas do computador quântico fotônico podem ser realizadas off-line, antes de entrar com os dados iniciais. De certa forma, o paralelismo do computador quântico permite que o cálculo seja realizado para todos os valores possíveis de X e Y ao mesmo tempo. Uma vez que determinamos que esse cálculo probabilístico funcionou, podemos escolher quais foram os dados iniciais. Dessa forma, podemos aumentar a probabilidade de sucesso do computador quântico fotônico para cerca de 100%. Nenhum computador clássico é capaz de fazer isso. O custo é um aumento considerável nos recursos necessários: muito mais fótons, mais interferômetros e detectores de alta qualidade.

Embora tenha havido muitos avanços desde o trabalho seminal de Feynman, um computador quântico "universal", capaz de realizar qualquer tarefa computacional, ainda é um sonho. Por outro lado, há aplicações mais restritas que estão sendo testadas hoje em dia. Uma dessas aplicações é a simulação quântica mencionada acima. Nesse contexto, simuladores fotônicos de baixa escala têm sido usados para emular diversos sistemas físicos, tais como pequenas moléculas e partículas interagentes (11;12). Existem, também, outros modelos de computação. Alguns destes são universais e outros foram desenvolvidos para resolver somente um conjunto muito restrito de problemas. Os computadores quânticos fotônicos têm sido explorados para investigar vários desses modelos (13).

Os avanços da ciência fundamental sempre acompanham os avanços da tecnologia, e vice-versa. Ocupando um papel importante na ciência e na indústria, a interferometria tem sido desenvolvida muito desde a época do Thomas Young. Hoje, a micro-fabricação de guias de onda permite a construção de interferômetros de muitos caminhos em um "chip" integrado, que ocupa uma área de somente alguns centímetros quadrados. Da mesma forma que a fenda dupla de Young permitiu a primeira observação de interferência com a luz, os interferômetros integrados prometem viabilizar a investigação de novos fenômenos de interferência, principalmente aqueles que dependem da natureza quântica da luz. Técnicas mais eficientes de produção de fótons estão sendo desenvolvidas, as quais darão acesso à investigação de interferência de mais fótons. É muito provável que a luz ainda guarde novos fenômenos inesperados. E, com certeza, serão muito bonitos.

 

Referências Bibliográficas

1. Talbot, H. F. "Facts relating to optical science", nº. IV, Philos. Mag. 9, 1836.

2. Farías, O. J.; Melo, F.; Milman, P.; Walborn, S. P. "Quantum information processing by weaving quantum Talbot carpets", ArXiv:1412.2710, 2014.

3. Clauser, J. F; Dowling, J. P. "Factoring integers with young's N-slit interferometer". Phys. Rev. A, vol. 53, nº.4587, 1996.

4. Taylor, Sir G. I. "Interference fringes with feeble light". Proc. Cam. Phil. Soc. 15: 114, 1909.

5. Aharanov, Y.; Davidovich, L.; Zagury, N. "Quantum random walks". Phys. Rev. A, vol.48, nº.1687, 1993.

6. Hong, C. K.; Ou, Z. Y.; Mandel, L. "Measurement of subpicosecond time intervals between two photons by interference". Phys. Rev. Lett., vol.59, nº. 2044, 1987.

7. Fonseca, E. J. S.; Monken, C. H.; Padua, S. "Measurement of the de broglie wavelength of a multiphoton wave packet". Phys. Rev. Lett., vol.82, nº.2868, 1999.

8. Feynman, R. "Simulating physics with computers". International Journal of Theoretical Physics, vol.21 (6-7), pp.467-488, 1982.

9. Milburn, G. J. "Quantum optical Fredkin gate". Phys. Rev. Lett., vol.62, nº.2124, 1989.

10. Knill, E.; Laflamme, R.; Milburn, G. J. "A scheme for efficient quantum computation with linear optics". Nature, vol.409, pp.46-52, 2001.

11. Aspuru-Guzik, A.; Walther, P. "Photonic quantum simulators". Nature Physics, vol.8, pp.285-291, 2012.

12. Georgescu, I. M.; Ashab, S.; Nori, F. "Quantum simulation". Rev. Mod. Phys., vol.86, nº.153, 2014.

13. Hogan, H. "Quantum computers appear: and are put to work". Photonics Spectra, June, 2013.