Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Ciência e Cultura
versão On-line ISSN 2317-6660
Cienc. Cult. vol.70 no.1 São Paulo jan./mar. 2018
http://dx.doi.org/10.21800/2317-66602018000100011
ARTIGOS
MATEMÁTICA
Percolação: problemas fáceis de enunciar e difíceis de resolver!
Bernardo N. B. de LimaI; Maria Eulália VaresII
IProfessor associado do Departamento de Matemática da Universidade Federal de Minas Gerais (UFMG). E-mail: bnblima@mat.ufmg.br
IIProfessora titular do Instituto de Matemática da Univerisdade Federal do Rio de Janeiro (UFRJ). E-mail: eulalia@im.ufrj.br
Se procurarmos nos principais dicionários da língua portuguesa, o termo percolação é sinônimo de lixiviação, que é o movimento de fluido em meio poroso, com o fluido extraindo substâncias solúveis do meio por onde "percola". Por exemplo, certamente já escutamos que as águas subterrâneas percolam no solo e entre as fraturas e fendas das rochas. Outro exemplo muito importante para nós matemáticos é o café: ao prepará-lo, a água percola através de um meio poroso, o pó de café, extraindo substâncias deste meio, o que é facilmente observado devido às mudanças de cor, odor e sabor do fluido.
Motivados por um problema aplicado - desenvolver um modelo probabilístico de máscaras de gás para trabalhadores de minas de carvão -, S. R. Broadbent e J. M. Hammersley, em 1957 [2], introduziram o modelo de percolação como o conhecemos em matemática. O meio poroso será um grafo 𝔾 = (𝕍, 𝔼) formado por um conjunto 𝕍 de vértices e um conjunto 𝔼 de elos, que são as ligações conectando pares de vértices. Uma imagem que podemos ter em mente é a de uma rede de canos (elos) como a que distribui água em nossas cidades. De um ponto de vista mais formal, o grafo mais utilizado é a rede hipercúbica d-dimensional, 𝕃d, cujos vértices são os pontos do espaço euclidiano d-dimensional com coordenadas inteiras e os elos unem dois vértices que diferem em apenas uma coordenada por uma unidade.
O caráter aleatório do modelo se manifesta atribuindo-se a cada elo o estado aberto ou fechado para a passagem do fluido. Em termos precisos, além do grafo temos um parâmetro, p, um número real no intervalo [0,1] que denota a probabilidade de cada elo estar aberto. O modelo de percolação de Bernoulli com parâmetro p é aquele em que cada elo está aberto com probabilidade p, fechado com probabilidade 1 - p, e os estados aberto e fechado para cada elo são variáveis aleatórias independentes. Em "matematiquês" o modelo é descrito pelo espaço de probabilidade (Ω, 𝒜 , ℙp), onde Ω= {0, 1}𝔼, o espaço amostral, é o conjunto com todas as configurações possíveis para os estados aberto (ou 1) e fechado (ou 0) dos elos; 𝒜 é a σ-álgebra gerada pelos eventos cilíndricos de Ωe ℙp é a medida de probabilidade subjacente - o subíndice p é para enfatizar que o estado de cada elo é 1 ou aberto com probabilidade p.
Dados dois vértices x, y ∈ 𝕍, dizemos que eles estão conectados em uma configuração ω∈ Ωse existe um caminho de elos abertos em Ωconectando os vértices x e y. Utilizaremos a notação (x↔y) para denotar o conjunto de tais configurações. Recorrendo à metáfora do fluido em meio poroso, em que o fluido penetra todos os elos abertos que encontra pela frente, dizer que x e y estão conectados quer dizer que se injetarmos fluido sob pressão no vértice x o vértice y ficará molhado. Dado um vértice x ∈ 𝕍 e uma configuração de elos abertos e fechados ω∈ Ω, definimos o aglomerado de x na configução ω, Cx(ω), como o conjunto dos vértices conectados a x por um caminho de elos abertos na configuração ω, isto é, os vértices que ficarão molhados ao introduzirmos o fluido em x; dito de modo mais preciso, Cx(ω) = {y ∈ 𝕍; x ↔y in ω}. Em grafos transitivos, como a rede hipercúbica d-dimensional 𝕃d, Cx é um conjunto aleatório cuja distribuição é a mesma para todo vértice x; desse modo, sem perda de generalidade podemos nos fixar em um vértice como a origem e denotaremos simplesmente por C o aglomerado da origem. Podemos pensar em ωcomo um subgrafo aleatório de 𝕃d, neste caso Cx(ω) seria a componente conexa de ωque contém o vértice x. A Figura 1 ilustra o modelo de percolação na rede quadrada.

A primeira pergunta que fazemos é sobre o tamanho do aglomerado C. Observe que seu número de vértices é um número natural, mas pode também ser infinito; logo, é natural surgir a pergunta: qual a probabilidade do aglomerado da origem ser infinito? Ou seja, para a variável aleatória C : Ω→ℕ∪{∞}, quanto vale ℙp {ω∈ Ω; #C(ω) = ∞}? Utilizaremos a notação mais curta (0 ↔ ∞) para denotar o evento {ω∈ Ω; #C(ω) = ∞}. Deste modo é natural definir a função θ(p), a probabilidade de percolação, como:
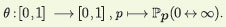
Como definida acima, a função θ(p) indica a probabilidade do aglomerado da origem ter tamanho infinito quando cada elo está aberto com probabilidade p. Podemos observar imediatamente que θ(0) = 0 e θ(1) = 1; além disso, é intuitivo acreditar que a função θ(p) seja monótona não decrescente em p. Esta última afirmação é verdadeira e sua demonstração pode ser vista no Capítulo 1 de [8], que é um texto clássico de percolação e referência básica para todos aqueles que queiram se iniciar ou aprofundar seus conhecimentos sobre o assunto.
Dada a monotonicidade da função θ(p), é natural definirmos o ponto crítico do modelo, pc, como aquele valor de p em que a função θ deixa de ser zero, isto é, pc = sup{p ∈ [0, 1]; θ(p) = 0}. Observe que o ponto crítico é uma característica do grafo; portanto, se considerarmos nosso grafo como a rede hipercúbica d-dimensional, temos que o ponto crítico é função da dimensão d. Deixamos como exercício para o leitor verificar que para d = 1 temos que pc = 1. O resultado abaixo, provado por Broadbent e Hammersley em [2], pode ser considerado um marco na teoria matemática da percolação:
Teorema 1 Considere um modelo de percolação de Bernoulli na rede hipercúbica d-dimensional com d > 2. Então existe pc = pc (d) ∈ (0, 1) tal que:
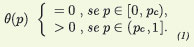
O teorema acima nos diz que há duas regiões bem distintas do intervalo [0,1]. O intervalo [0, pc) é a fase subcrítica onde a probabilidade da origem percolar é zero e o intervalo (pc, 1], a fase supercrítica, onde a probabilidade da origem percolar é estritamente positiva. O teorema nada diz sobre o que ocorre no ponto crítico.
Quando d = 2 foi provado por H. Kesten [11] que pc = ½. De fato a prova deu-se em duas partes e passaram-se vinte anos entre ambas: em [10] T. Harris provou que θ(½) = 0 (em particular pc > ½). Em dimensões altas, d > 19, T. Hara e G. Slade [9] provaram, utilizando a técnica conhecida com expansão em laços, que a probabilidade de percolação no ponto crítico também é zero. Acredita-se que o mesmo seja válido para todo d > 2. Determinar se θ (pc(d)) = 0 para 3 < d < 18 é um problema ainda em aberto e certamente um dos problemas mais importantes da probabilidade atual.
Na discussão acima, os estados de elos distintos (aberto ou fechado) representam variáveis aleatórias independentes. A consideração de uma classe importante de medidas mais gerais liga percolação a modelos oriundos da mecânica estatística. O exemplo mais básico corresponde ao clássico modelo de Ising na rede quadrada (estende-se a outros grafos e aos chamados modelos de Potts). Daqui até o final desta seção, este será sempre o nosso grafo, 𝕃2. No modelo de Ising atribui-se a cada vértice x uma variável aleatória σx que pode tomar dois valores, +1 ou -1, simulando duas possíveis orientações de um spin. Tomando-se uma caixa finita Λ = [-L, L] × [-L, L] em 𝕃2 considera-se uma função energia que favorece o alinhamento de spins: um elo entre vizinhos com mesmo spin contribui com -1 para a energia; caso contrário, contribui com +1. A energia HΛ(σ) fica então 2n(σ)-NΛ, onde n(σ) é o número de elos que conectam vértices com spins distintos e NΛ é uma constante, simplesmente o número total de elos no grafo restrito a Λ (irrelevante na definição abaixo). Define-se uma medida de probabilidade no conjunto de todas as configurações de spins na caixa Λ
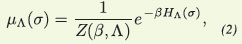
onde β> 0 representa o inverso da temperatura e Z(β, Λ) é a constante de normalização para que os pesos somem 1. Note que valores grandes de β(baixas temperaturas) favorecem as configurações de menor energia, ao passo que para valores altos da temperatura (βpequeno), a entropia tem um papel mais importante, fazendo com que a medida tenda a ficar mais próxima de uma medida uniforme no conjunto de todas as configurações. Esse jogo entre energia e entropia determina a existência de uma temperatura crítica, que pode ser caracterizada da seguinte forma no caso do modelo de Ising: coloca-se uma condição externa constante e.g. toma-se σx=+1 para todo x na fronteira da caixa Λ e seja µΛ+ a medida assim obtida. Existe um valor crítico βc tal que o valor médio de σ0 na origem tende a zero quando L tende a infinito se β< βc, e tende a um valor positivo m+ (β) se β> βc. Em outras palavras, existe uma memória de longo alcance (o spin na origem lembra o que há na fronteira cada vez mais distante) abaixo da temperatura crítica. Uma versão disto se aplica também quando σx toma valores em {1, 2, ..., q}, q > 2 inteiro, o que é conhecido como modelo de Potts.
A transição de fase no modelo de Ising também pode ser formulada ignorando condições externas, mas acrescentando um termo do tipo h Σ σx à energia, onde h representa um campo magnético e a soma é sobre x ∈ Λ. Da mesma forma, quando a temperatura 1/ βestiver abaixo de 1/ βc observa-se uma "magnetização espontânea", ou seja, o valor médio do spin na origem no limite L → ∞ é uma função m(β,h) que tende a m+(β) (-m+(β)) quando h tende a zero por valores positivos (negativos, respectivamente). A existência de βc (finito e positivo) foi inicialmente obtida por R. Peierls [15], sendo que L. Onsager [14] determinou o valor exato para o modelo de Ising. Onsager provou ademais que na temperatura crítica o valor médio, sob µΛ+, do spin na origem tende a zero quando o volume cresce, i.e. L → ∞. Isto sem dúvida nos remete ao resultado de Harris-Kesten, e seria natural buscar pela relação entre os dois. Para isso precisamos olhar os modelos de forma mais geral.
C. M. Fortuin e P. W. Kasteleyn [6] introduziram, no final dos anos 1960, uma classe de medidas de percolação que generalizam as medidas ℙp consideradas anteriormente. Dependem de dois parâmetros: p como antes e q ∈ (0, +∞). Para p, q fixados, e restrita a um volume finito Λ a probabilidade de uma configuração de elos ω∈ {0, 1}𝔼(Λ) é dada por
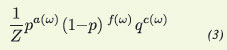
onde a(ω) (f(ω)) representa o número de elos abertos (fechados), c(ω) representa o número de aglomerados (ou componentes conexas) de ω, e Z =Z (Λ, p, q) é novamente a constante de normalização. O parâmetro q introduz uma dependência de longo alcance. Consideraremos apenas o caso q > 1. Quando q = 1 temos simplesmente ℙp.
Se q = 2 e p = 1 - e -βpodemos associar uma configuração de spins atribuindo o mesmo spin σx para todos os vértices x em cada dado aglomerado de ω, com probabilidade 1/2 e independente ao variarmos os aglomerados. Com isto recupera-se o modelo de Ising nos spins [5]. Para considerar condições externas constantes nos spins, podemos pensar que todos os elos com pelo menos um vértice fora de Λ estejam abertos e nesta componente infinita os spins sejam todos iguais à condição externa (+1 ou -1). Em 𝕃2, estendendo a notação acima, tem-se ainda θ(pc(2), 2) = 0, o que corresponde à unicidade da medida na temperatura crítica, como provada por Onsager; o valor pc(q)= 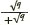 determina a temperatura crítica para o modelo de Potts em 𝕃2. A relação entre a percolação de Fortuin- Kasteleyn e o correspondente modelo de spins (Ising/Potts) tem sido muito explorada em pesquisa recente, especialmente no caso planar, com resultados importantes, confirmando outra conjectura famosa, devida a R.J. Baxter: θ(pc(q); q) = 0 vale para q < 4 ([3] e referências) ao passo que para q > 4 a transição de fase é descontínua, i.e. θ(pc(q), q) > 0 [4]. Conjectura-se resultado análogo para dimensões maiores, com uma função Q(d) no lugar de q = 4 acima.
determina a temperatura crítica para o modelo de Potts em 𝕃2. A relação entre a percolação de Fortuin- Kasteleyn e o correspondente modelo de spins (Ising/Potts) tem sido muito explorada em pesquisa recente, especialmente no caso planar, com resultados importantes, confirmando outra conjectura famosa, devida a R.J. Baxter: θ(pc(q); q) = 0 vale para q < 4 ([3] e referências) ao passo que para q > 4 a transição de fase é descontínua, i.e. θ(pc(q), q) > 0 [4]. Conjectura-se resultado análogo para dimensões maiores, com uma função Q(d) no lugar de q = 4 acima.
PERCOLAÇÃO EM OUTRAS QUESTÕES
Diremos que um par (η, ξ) de sequências binárias η= (η1, η2, ...) e ξ= (ξ1, ξ2, ... ) é compatível se for possível extrair uns de ηe zeros de ξde modo que sobrem duas sequências infinitas idênticas. Fácil dar exemplos de pares compatíveis bem como de pares incompatíveis: η= 1 fica evidentemente compatível com qualquer sequência ξque tiver infinitos uns. Motivado por questões oriundas de agendamento em computação, P. Winkler [16] formulou o seguinte problema: supondo que ηn e ξm sejam todas variáveis aleatórias independentes, sendo que ηn (ξn) vale 1 com probabilidade q (p) e vale 0 com probabilidade 1 - q (1 - p, respectivamente), podemos encontrar 0 < q, p < 1 de modo que o par seja compatível com probabilidade positiva? Trata-se pois da medida de probabilidade ℙq × ℙp em {0, 1}ℕ x {0, 1}ℕ e pergunta-se se o conjunto dos pares compatíveis (η, ξ) tem probabilidade positiva. Espera-se uma resposta afirmativa se q próximo a 1 e p próximo a zero. Isto foi provado em [7] e [1].
Cabe perguntar se podemos construir uma sequência ηcom densidade positiva de zeros, e que seja compatível com um conjunto de probabilidade positiva para ℙp (o que chamamos p-compatível). Uma resposta abstrata decorre do resultado acima (pelo teorema de Fubini), mas ainda cabe perguntar se podemos construir uma tal sequência explicitamente. Uma resposta parcial foi dada em [13], onde se constrói uma sequência com muitos zeros em um sentido mais fraco (dimensão de Hausdorff) que é p-compatível. Interessa salientar aqui que o problema pode ser visto como uma questão de percolação, ou seja, a existência de um caminho infinito aberto, a partir de um dado vértice. Há duas diferenças fundamentais em relação ao que tratamos antes: (i) mais natural pensar que agora são os vértices (em vez dos elos) que podem estar abertos ou fechados, e ademais os caminhos devem agora ser orientados em algum sentido, pois precisamos percorrer as sequências na ordem dada; (ii) as variáveis em uma mesma coluna são extremanente dependentes, em contraste com o exemplo discutido inicialmente. De fato a construção é feita em 𝕍 = {0, 1, 2 ...}2, após convenientemente utilizar uma transformação, η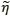 , ξ
, ξ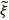 , das sequências binárias η, ξque supomos terem infinitos zeros e infinitos uns. As coordenadas de η
, das sequências binárias η, ξque supomos terem infinitos zeros e infinitos uns. As coordenadas de η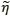 e ξ
e ξ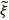 são os sucessivos comprimentos das filas de uns entre dois zeros sucessivos em η, ξ. Um vértice (u, v) será declarado aberto se η
são os sucessivos comprimentos das filas de uns entre dois zeros sucessivos em η, ξ. Um vértice (u, v) será declarado aberto se η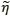 u> ξ
u> ξ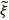 v, de onde vemos a dependência em cada coluna. A Figura 2 ilustra com simulações correspondentes a (η, ξ) Bernoulli.
v, de onde vemos a dependência em cada coluna. A Figura 2 ilustra com simulações correspondentes a (η, ξ) Bernoulli.

Há várias questões envolvendo sequências aleatórias que podem ser colocadas dessa forma. Não vamos entrar nos detalhes do exemplo. O que pudemos fazer com este método foi: para cada 𝜖 > 0 construímos uma sequência η𝜖 cujo conjunto de zeros é um fractal de dimensão de Hausdorff pelo menos 1- 𝜖 e para o qual podemos tomar p𝜖 > 0 de modo que η𝜖 será p-compatível, para todo p > p𝜖.
REFERÊNCIAS
1. Basu, R.; Sly, A. "Lipschitz embeddings of random sequences". Probab. Theory Relat. Fields 159, 721-775, 2014.
2. Broadbent, S. R. and Hammersley, J. M. "Percolation process I. Cristals and mazes". Proceedings of the Cambridge Philosophical Society 53, 629-641, 1957.
3. Duminil-Copin, H. "Parafermionic observables and their applications to planar statistical physics models", Ensaios Matemáticos 25, Brazilian Mathematical Society, 2013.
4. Duminil-Copin, H.; Gagnebin, M.; Harel; M.; Manolescu, I.; Tassion, V. "Discontinuity of the phase transition for the planar random-cluster and Potts models with q>4". arXiv:1611.09877.
5. Edwards, R. G. and Sokal A. D. "Generalization of the Fortuin-Kasteleyn-Swendsen-Wang representation and Monte Carlo algorithm". Phys. Rev D. 38, 2009-2012, 1988.
6. Fortuin, C. M. and Kasteleyn, P.W. "On the random cluster model I. Introduction and relation to other models". Physica 57, 536-564, 1972.
7. Gács, P. "Compatible sequences and a slow Winkler percolation". Combin. Probab. Comput. 6, 815-856, 2004.
8. Grimmett, G. R. Percolation, 2nd edition. Springer-Verlag, Berlin, 1999.
9. Hara, T. and Slade, G. "Mean field critical behavior for percolation in high dimentions". Communications in Mathmatical Physics 128, 333-391, 1990.
10. Harris, T.E. "A lower bound for the critical probability in a certain percolation process". Proc. Cam. Philos. Soc. 56, 13-20, 1960.
11. Kesten, H. "The critical probability of bond percolation on the square lattice equals 1/2". Communications in Mathmatical Physics 74, 41-59, 1980.
12. Kesten, H. Percolation theory for mathematicians. Birkhäuser, Boston, 1982.
13. Kesten, H.; de Lima, B. N. B.; Sidoravicius, V.; Vares, M. E. "On the compatibility of binary sequences". Communications on Pure and Applied Mathematics (Print), 67, 871-905, 2014.
14. Onsager, L. "Crystal statistics. I. A two-dimensional model with an order-disorder transition". Phys. Rev. 65, 117-149, 1944.
15. Peierls, P. "On Ising's model of ferromagnetism". Math. Proc. Camb. Phil. Soc. 32, 477-481, 1936.
16. Winkler, P. "Dependent percolation and colliding random walks". Random Structures & Algorithms 16, 58-84, 2000.